Boolean Algebra

Digital Circuits

Two voltage levels

• High/ Low
• 1/ 0

Two Types

• Combinational: no memory
  • Multiplexers
• Sequential: with memory
  • Counters, registers

Boolean Algebra

Boolean Values

• True
• False

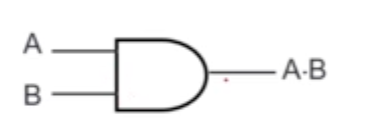
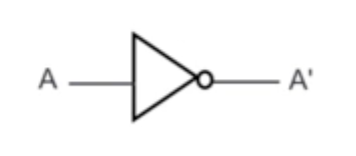
Connectives and their logic gates

• Conjunction (AND)
  • $A\cdot B$
  • 
• Disjunction (OR)
  • $A+B$
  • 
• Negation (NOT)
  • $A^{\prime }$
  • 

Precedence of Operators

Highest Precedence to lowest

1. Not
2. And
3. Or

Laws of Boolean Algebra

Identity Laws

$A+0=0+A=A$ $A\cdot 1=1\cdot A=A$

Inverse/ complement laws

$A+A^{\prime }=A^{\prime }+A=1$ $A\cdot A^{\prime }=A^{\prime }\cdot A=0$

Commutative laws

$A+B=B+A$ $A\cdot B=B\cdot A$

Associative laws

$A+(B+C)=(A+B)+C$ $A\cdot (B\cdot C)=(A\cdot B)\cdot C$

Distributive laws

$A\cdot (B+C)=(A\cdot B)+(A\cdot C)$ $A+(B\cdot C)=(A+B)\cdot (A+C)$

Duality

• if the AND/OR operators and identity elements 0/1 in a Boolean equation are interchanged, it remains valid.
• Gives free theorems - “two for the price of one”, as a Boolean equation is logically equivalent to its dual. SO, you prove one theorem and the other comes for free!

Warning

Duality is not the same as Complement Functions

Theorems

• Idempotency, one element, involution, absorption, demorgans, consensus

Boolean Functions

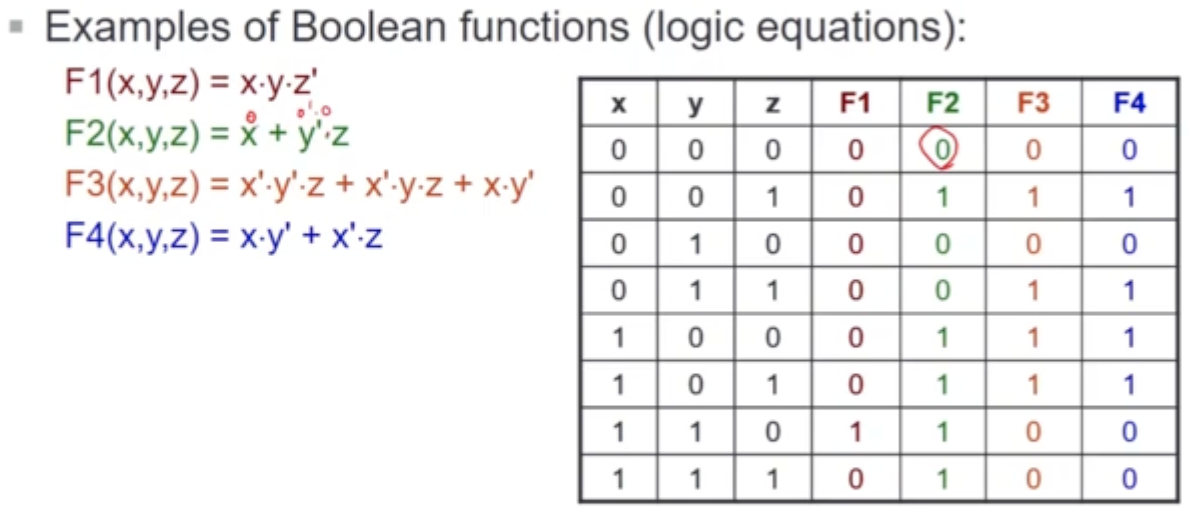
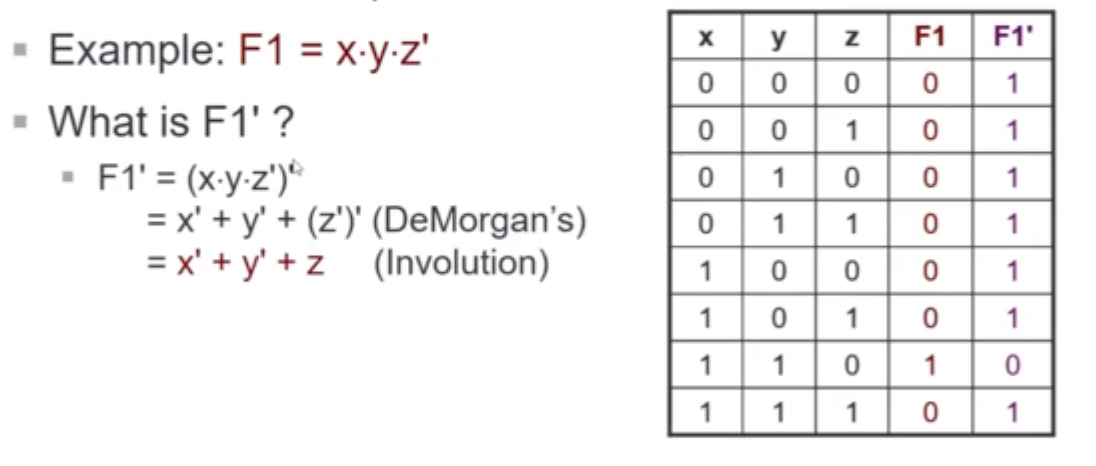
Complement Functions

• Given a boolean function F, the complement of F denoted as F’, is obtained by interchanging 1 with 0 in the function’s output values
• 

Standard Forms

Literals

A Boolean variable on its own or in its complemented form

Product Term

A single literal or a logical product (AND) of several literals

Sum term

• A single literal or a logical sum (OR) of several literals

Sum-of-Products (SOP) expression

• A product term or a logical sum (OR) of several product terms

Product-of-Sums (POS) expression

• A sum term or a logical product (AND) of several sum terms

Note

Every boolean expression can be expressed in SOP or POS form

Minterms and Maxterms

Minterm

• A minterm of n variables is a product term that contains n literals from all the variables
  • e.g. On variables x and y, the min terms are
    • $x^{\prime }\cdot y^{\prime }$
    • $x\cdot y^{\prime }$
    • $x^{\prime }\cdot y$
    • $x\cdot y$

Maxterm

• a maxterm of n variables is a sum term that contains n literals from all the variables
  • e.g. On variables x and y, the maxterms are
    • $x^{\prime }+y^{\prime }$
    • $x+y^{\prime }$
    • $x^{\prime }+y$
    • $x+y$

General

• in general, with n variables, we have up to $2^n$ minterms and $2^n$ maxterms
• 
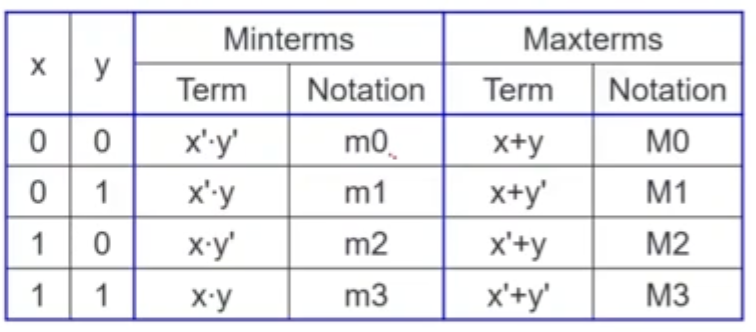
• Trick for minterm: x’ dot y’ is m0 because 00 in binary is 0
• likewise, x dot y’ is m2 because 10 in binary is 2
• Complement: 0
• non-complement: 1

Important

Each minterm is the complement of its corresponding maxterm. Likewise, each maxterm is the complement of its corresponding midterm.

Canonical Forms

Sum-of-minterms = Canonical sum-of-products

Product-of-maxterms = Canonical product-of-sums

Conversion