Simplification

Function Simplification

Why?

• fewer logic gates
• cheaper, less power, faster

Techniques

• Algebraic
• Karnaugh Maps
• Quine-McCluskey

Algebric Simplification

Aim

Minimise

• number of literals (priority)
• number of terms

Example 1

Example 2

Half Adder

• circuit that adds 2 single bits (X, Y) to produce a result of 2 bits (C, S).
• 
• In canonical form (sum of minterms):
  • $C=X\cdot Y$
  • $S=X^{\prime }\cdot Y+X\cdot Y^{\prime }$
    • OR S can be thought of as the exclusive OR operation

Gray Code/ Reflected binary code

• Unweighted
• Only a single bit change from one code value to the next
• n bits → $2^n$ values
• Good for error detection
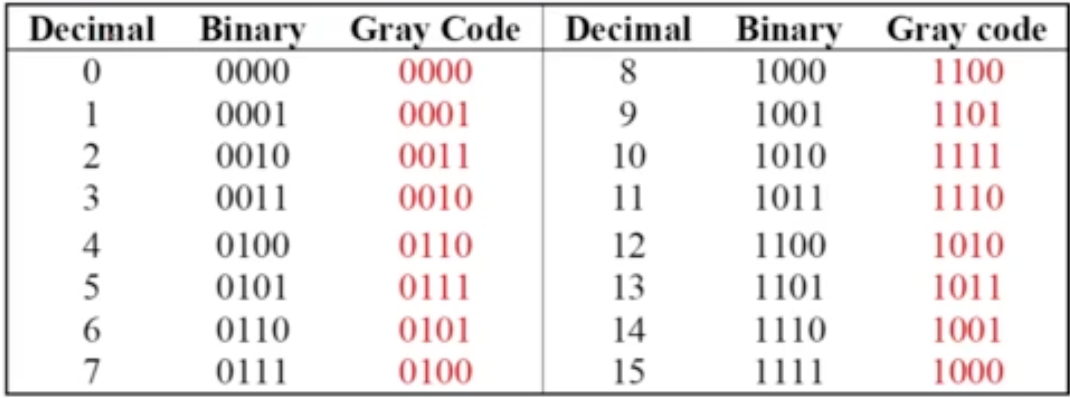• Generating a 4-bit standard Gray code sequence
• The “reflection” technique
• 

K-Maps

Introduction

• Systematic method to obtain simplified sum-of-products (SOP) expression

Layouts of 2-Variable (a, b) k-map:

or you can use

• 1 for a / b
• 0 for a’ / b’

Layouts of 3-Variable K-Maps

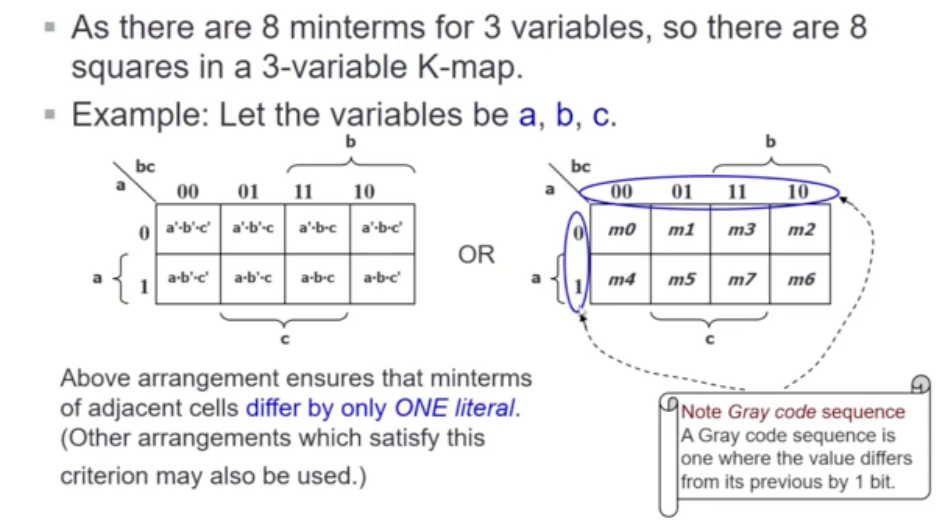
• There is a wrap around
  • neighbour of m0 = m1, m2, m4
• In general: every n-variable k-map has n adjacent neighbour

Layouts of 4-variable K-Map

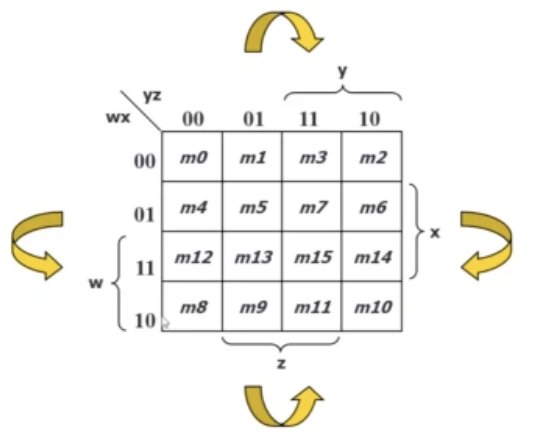
• wrap around works here!

Layout of 5-variable K-Map

• organised as two 4-variable K-maps
• one for v and another one for v’
• 
• Wrap around also applies here
  • Neighbours of m0 = m1, m4, m2, m8 and m16
  • This is because m0 and m16 differ by v’/ v (1 literal)

Larger K-Maps

• four 4-variable k-map
• 
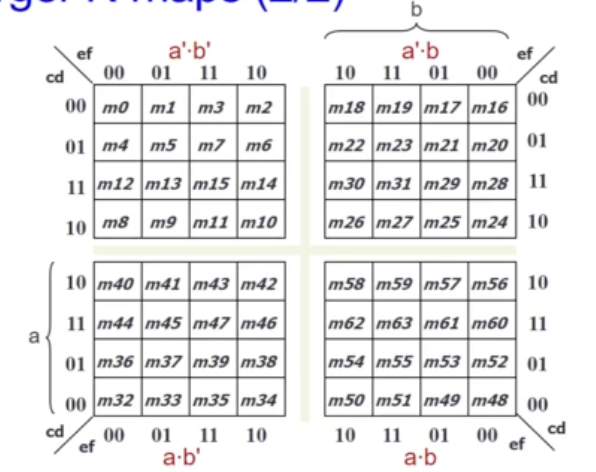
• it becomes increasingly complex to look for neighbours

How to use the K-Map?

Recall Unifying Theorem:

$$A+A^{\prime }=1$$

• In a K-map, each cell containing a ‘1’ corresponds to a minterm of a given function F where the output is 1.
• Each valid grouping of adjacent cells containing ‘1’ then corresponds to a simpler product term of F
  • A group must have size in powers of two: 1, 2, 4, 8
  • In general, grouping $2^n$ cells eliminates n variables
• Group as many cells as possible
• Select as few groups as possible to cover all the cells (minterms) of the function
• 

Converting to Minterms Form

Given a boolean function, you can convert into minterm form following this two steps

1. Convert to sum of product form
2. Apply to K-Map

Simpliest SOP Expression from K-Map

Need to obtain

1. Minimum number of literals per product term
2. Minimum number of product terms

Achieved using

1. Bigger groupings of minterms (prime implicants) where possible
2. No redundant groupings (look for essential prime implicants)

Keyword implicant: any combination of variables that accounts for one or more minterms of the function

Prime Implicant: A fully combined implicant, meaning it cannot be combine with another to further eliminate variables

Essential Prime Implicant: A prime implicant that includes at least one minterm that is not covered by any other prime implicant

Positive/ Negative examples of prime implicant:

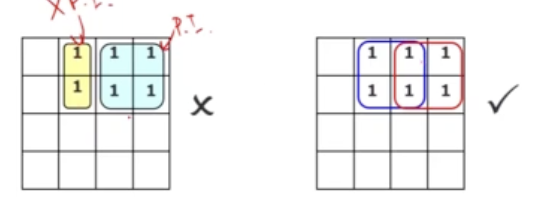
Find Simplifed SOP from K-Map

Algorithm

1. Circle all prime implicants on the K-Map
2. Identify and select all essential prime implicants for the cover.
3. Select a minimum subset of the remaining prime implicants to complete the cover, that is, to cover those minterms not covered by the essential prime implicants

Find Simplified POS from K-Map

Instead of grouping the minterms, you group the maxterms (i.e. the 0s)

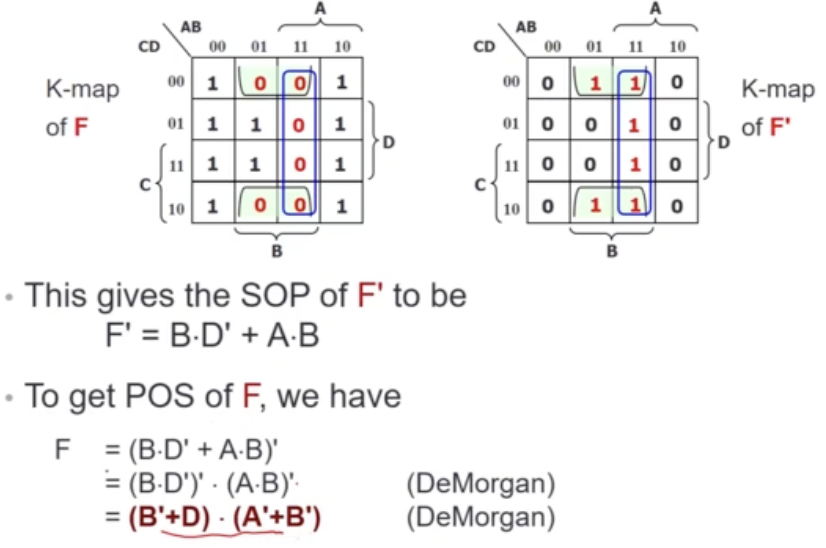
• Note that complementing SOP will give POS

Don’t-Care Conditions

$$F(A,B,C)=\sum m(3,5,6)+\sum d(0,7)$$ $$G(A,B,C)=\sum m(1,2,4)+\sum d(0,7)$$

You may treat “don’t cares” as 1 or 0s in K-Maps

• can lead to shorter expressions