Combinational Circuits

Introduction

Combinational Circuits

• Each output depends entirely on the immediate present (inputs)

Sequential Circuit

• Each output depends on both present inputs and state

Analysis Procedure

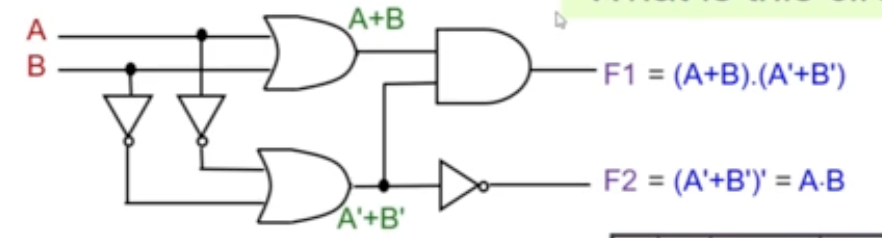
1. Label the inputs and outputs
2. Obtain the functions of intermediate points and the outputs
3. Draw the truth table
4. 
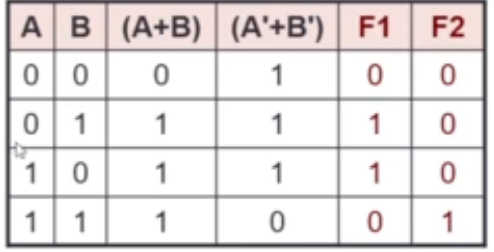
5. Deduce the functionality of the circuit

Design Methods

Different methods

• Gate-level (with logic gates)
• Block-level (with functional blocks)

Main Objectives

• Reduce cost
• increase speed
• Design simplicity

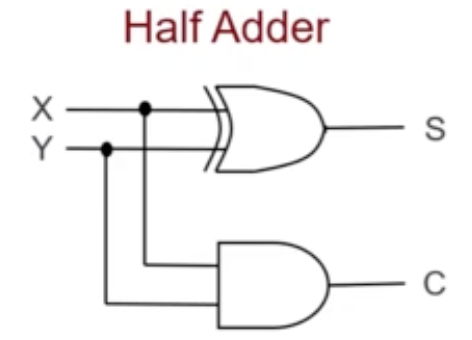
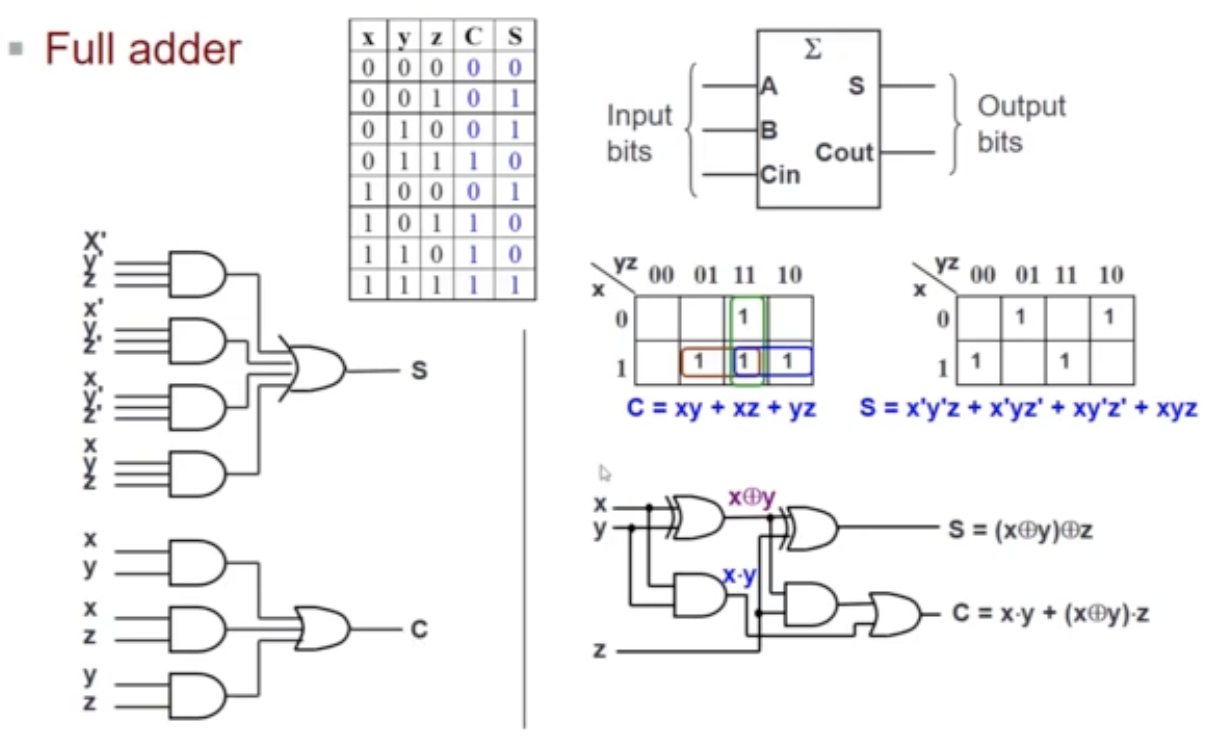
Gate-Level (SSI) Design: Half Adder

1. State Problem → Half Adder
2. Determine and label the inputs and outputs of the circuit
3. Draw the truth table
4. Obtain simplified Boolean Functions (can use K-Maps!)
   • e.g.
   • $C=X\cdot Y$
   • $S=X\oplus Y$
5. Draw logic diagram

Block-Level Design

More complex circuits can also be built using block-level method.

• Generally, block-level design method relies on algorithms or formulae of the circuit, which are obtained by decomposing the main problem to sub-problems recursively

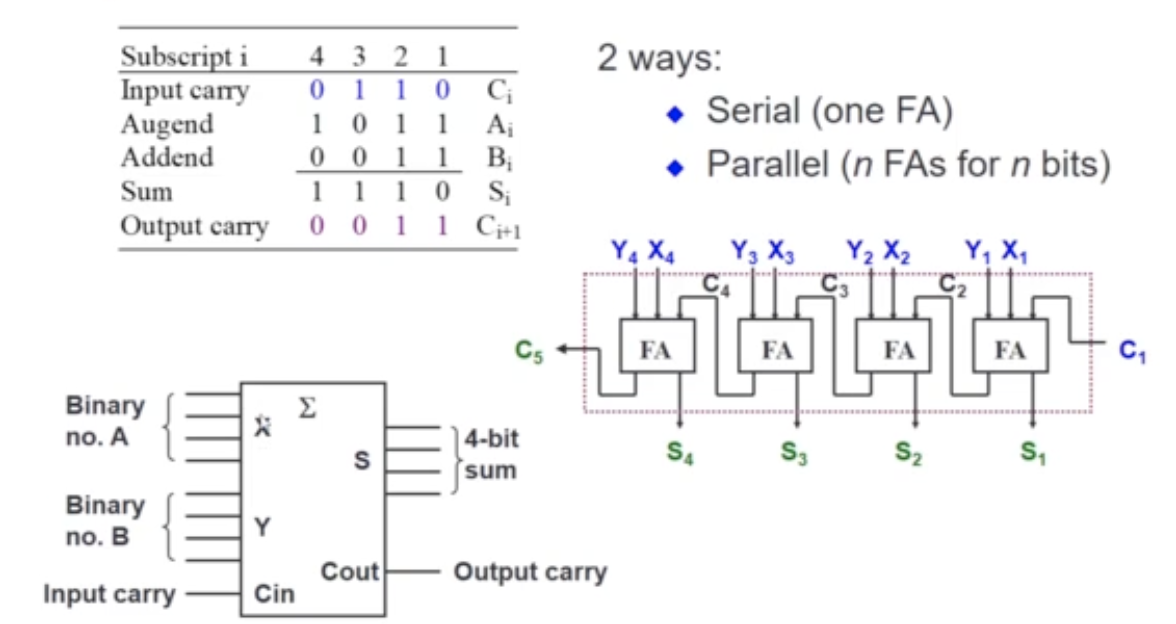
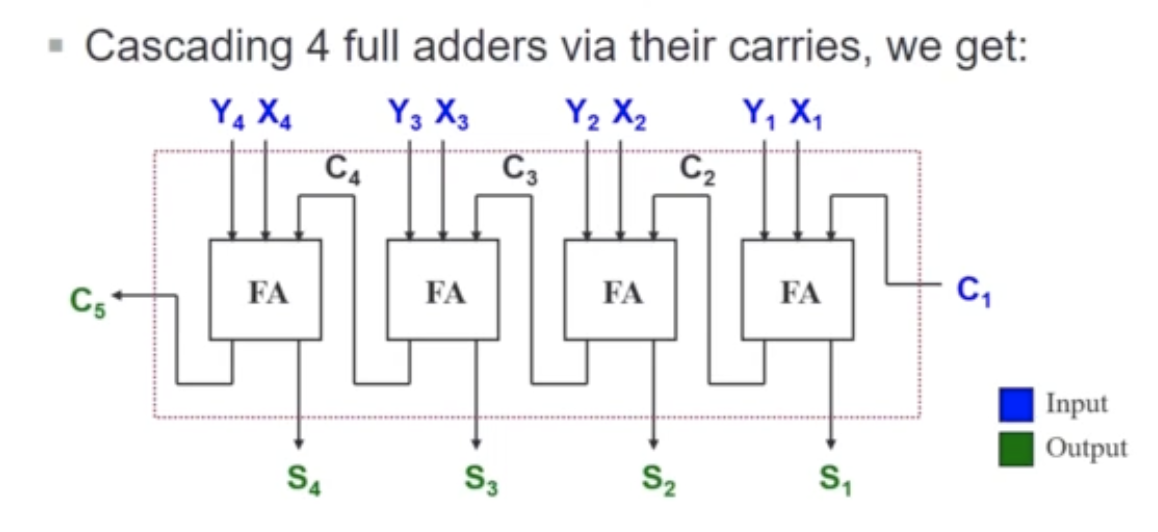
4-bit Parallel Adder

• Circuit to add two 4-bit numbers together and a carry-in, to produce a 5-bit result
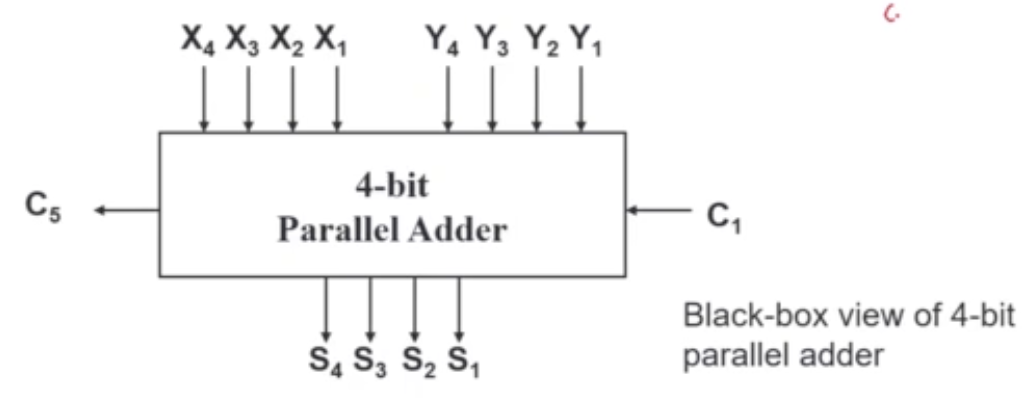
• If you were to try to construct the truth table, you realise that it is too big, there are $2^9=512$ rows!
• Simplification becomes too complicated!
• We note that we can obtain Excess-3 code with the parrallel adder
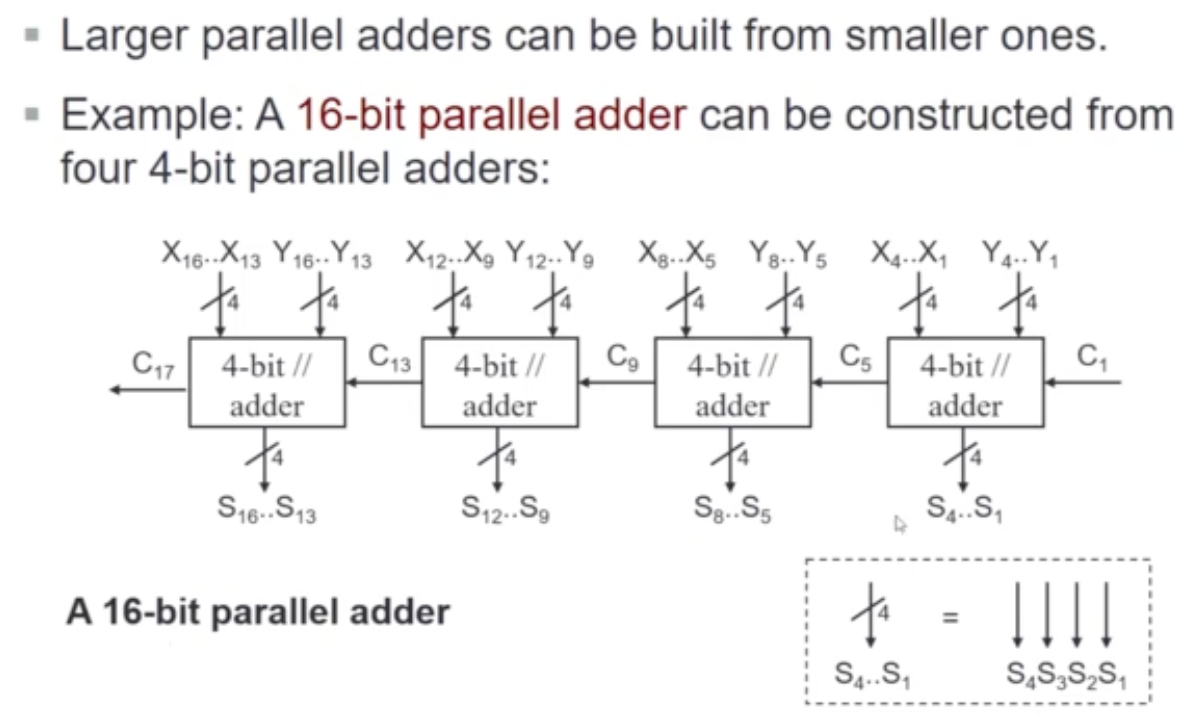
• You can also build a 16-bit parallel adder with a 4-bit parallel adder!

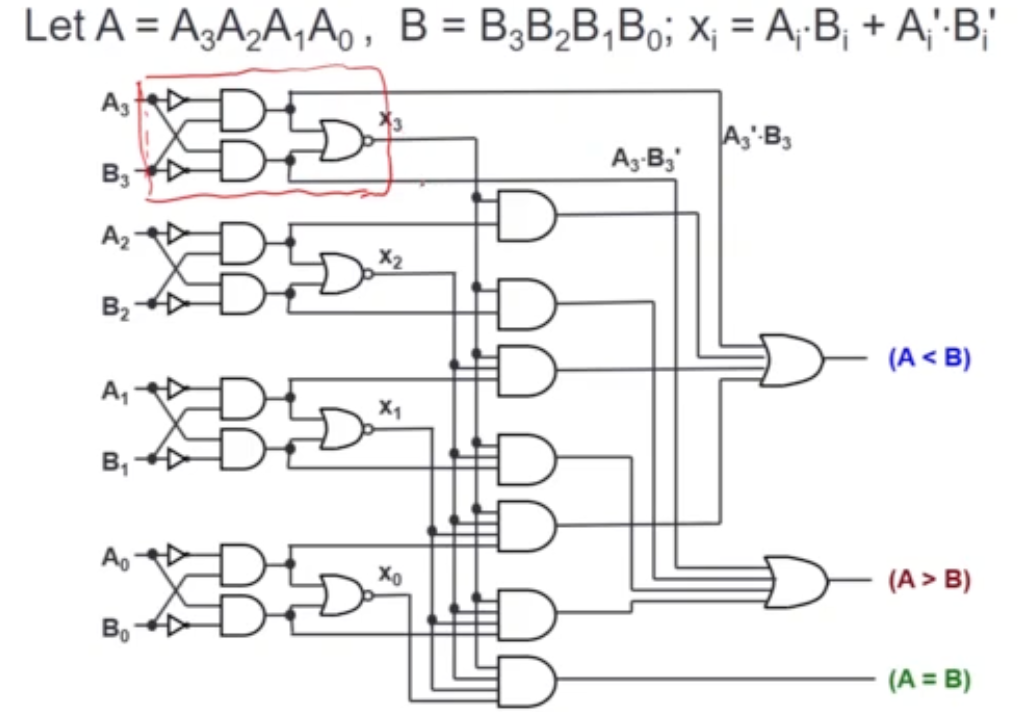
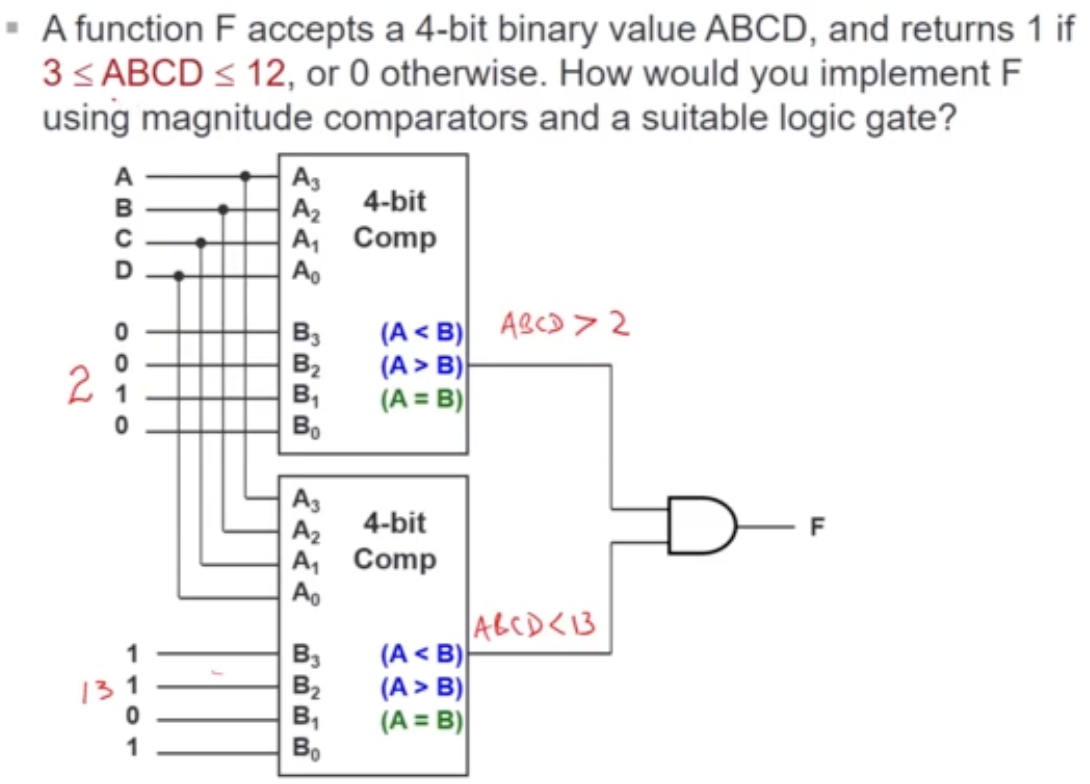
Magnitude Comparator

• compare 2 unsigned values A and B, to check if A > B, A=B, or A < B
• To design an n-bit magnitude comparator using classical method, it would require $2^{2n}$ rows in the truth table
• This is simply too much!

Analysis

1. if MSBA > MSBB, then A > B
2. Likewise for the remaining bits

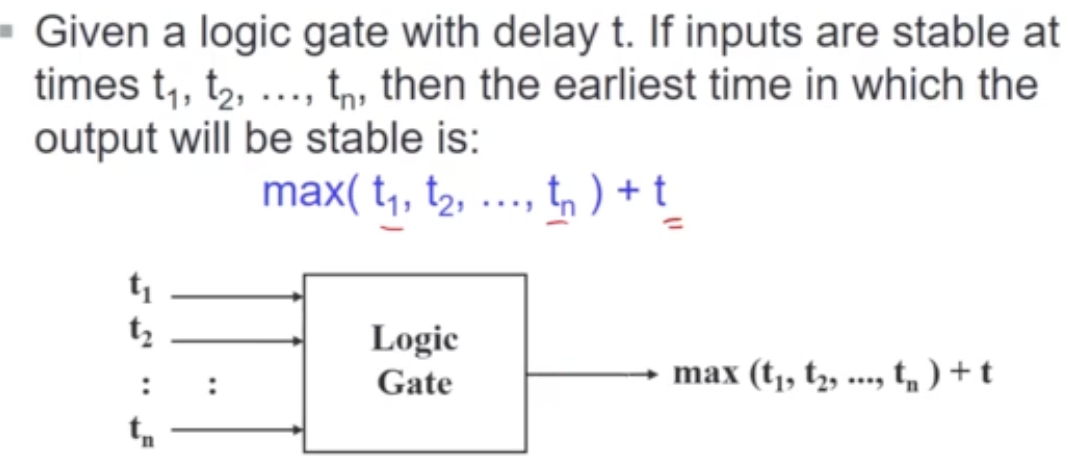
Circuit Delay

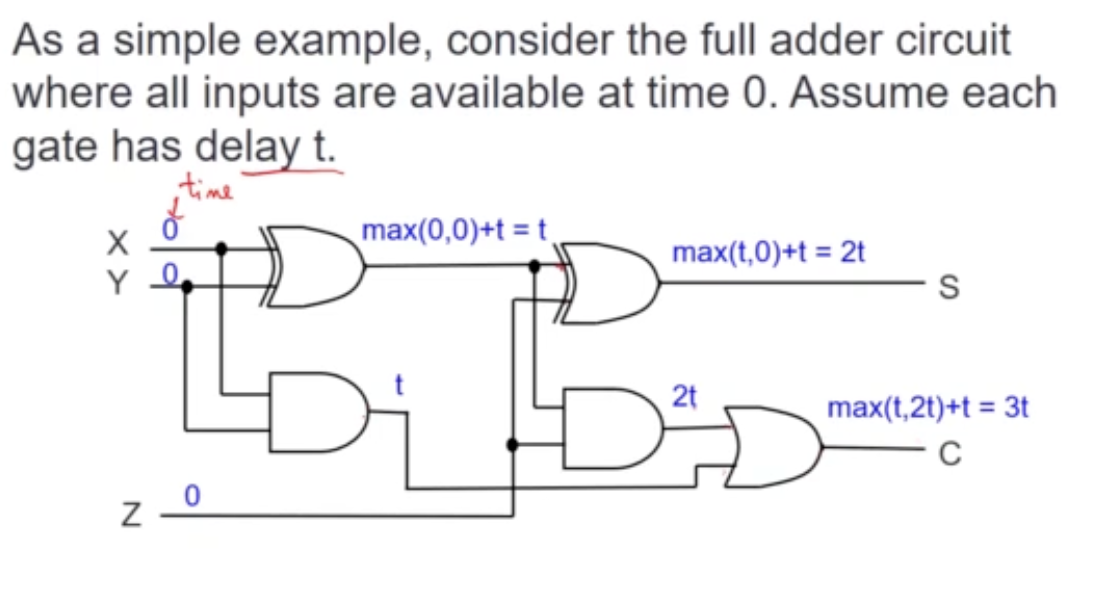
Summary of Arithmetic Circuits

Half Adder

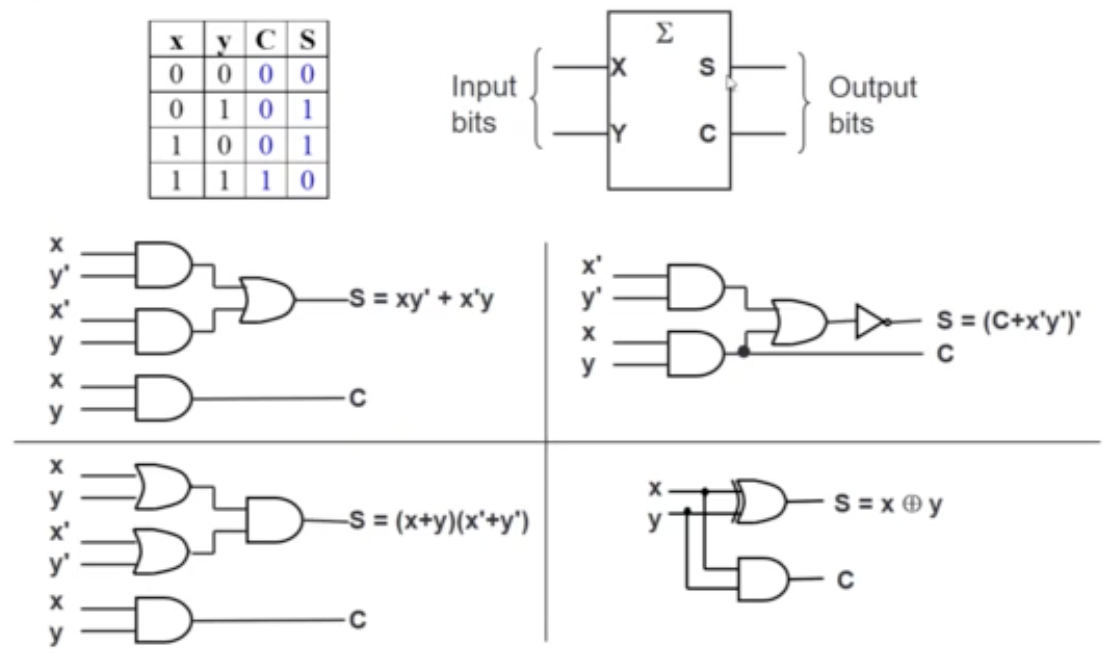
Full Adder

4-bit parallel Adder